Distinct relaxation dynamics

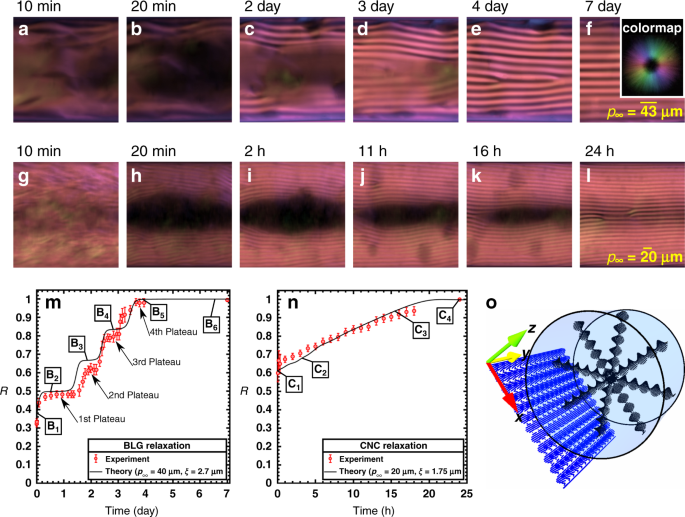
Figure 1a–l shows the sequences of microscopy images analyzed by PolScope⁴⁴. The analysis allows extrapolating the average of fibers’ orientation over the thickness of capillary tube and the two-dimensional (2D) fibers’ orientation is represented according to the colormap shown in Fig. 1f; for example, the pink color which is ubiquitous in the POM images indicates that fibers are aligned parallel to the central axis (y-axis) (Fig. 1a–l, o). Initially (right after filling capillaries), the fibrils located close to the center of the cylindrical capillary form a para-nematic phase with a director field parallel to the central axis of the cylinder due to flow-induced alignment during capillary filling (described by pink color). Shortly thereafter (within the first 20 min), dark zones emerge in the center of the capillaries and some cholesteric fingerprints are already visible near the walls.

a–f Time-series snapshots of BLG microscopy (POM) images. g–l Time-series snapshots of CNC microscopy (POM) images. The images shown in panels a–l were experimentally acquired using the LC PolScope device and different colors represent different director field orientations which are appreciated according to the colormap depicted as the inset in the panel f. See Supplementary Note 1 for the detailed discussion on the mapping between fibers orientation and colormap. Note that the colormap shown as the inset in the panel f is applicable for all the microscopy images studied in this work. Over the relaxation time, cholesteric fingerprints progressively propagate into the unwound state (dark zone). Times elapsed from the beginning of relaxation are shown on top-left corners; min and h stand for minutes and hours, respectively. m Experimental observation and numerical simulation on the normalized relaxation progress curve, R, for BLG. The labels B₁ to B₆ correspond to Fig. 2. n Experimental observation and numerical simulation on the normalized relaxation progress curve, R, for CNC. The labels C₁ to C₄ correspond to Fig. 3. o The coordinate system used throughout this study along with a schematic illustration of a capillary tube indicating the ground state of fibers configuration in a circular cross-section in the xz-plane, known as concentric, and the averaged fibers configuration in a lateral plane in the xy-plane, known as chiral monodomain. The averaged fibers configuration on the lateral plane is representative of the colormap PolScop analysis shown in the panels a–l.

During equilibration, chiral fronts form and propagate from the wall inwards and gradually replace the dark areas, showing how the system is progressively equilibrated by the self-reconstruction of unwound chiral helices (Fig. 1a–l and Supplementary Movies 1 and 2). The physical origin of the initial dark areas emerging from the para-nematic phase cannot be interpreted unequivocally since the absence of birefringence can correspond to different scenarios. In fact, the fibers’ orientation in the dark areas (i.e. capillary middle) can represent three different situations: (1) fibers do not possess mesogenic correlation and the phase could be isotropic although the fibers’ concentration is a constant equal to the cholesteric bulk (i.e. the upper binodal miscibility boundary); (2) fibers are aligned normal to the plane and thus the phase is nematic; (3) the cholesteric helices are aligned normal to the plane and the light path, thus the phase could be already cholesteric. Determining the fibers’ configuration in the dark areas is addressed below.

To rationalize the observations, we define the dimensionless normalized relaxation progress: \(R\left( t \right) = \frac{{\bar q\left( t \right)}}{{q_\infty }}\), where \(\bar q\left( t \right) = \frac{{{\mathrm{2}}\pi }}{{\bar p\left( t \right)}}\), \(\bar q\left( t \right)\) and \(\bar p\left( t \right)\) are the spatially averaged chiral wavevector and pitch length, respectively. This quantity, R, provides insight into the amount of space occupied by the cholesteric phase at any given time in the system. The relaxation progress, R, ranges from 0 to 1; for R = 0, there is no chiral nematic phase in the system, and when R = 1, the chiral nematic phase fills the sample and the system reaches the ground state. To obtain \(\bar q\left( t \right)\), each time-series POM snapshot is partitioned into approximate monodomains, and \(\bar q\left( t \right)\) is then computed as the weighted average of local chiral wavevectors: \(\bar q(t) = {\sum} {\frac{{A_iq_i}}{A}}\) where A, A_i, and q_i indicate the total area of the snapshot, area of the cholesteric zone, and chiral wavevector for the ith partition, respectively. Figure 1m, n shows the time evolution of R for BLG and CNC, respectively. R starts with an initial value representing the chiral nematic layers that are near the bounding surface at the very beginning of the experiment. Eventually, R reaches unity, indicating the equilibration is complete all over the field of view and the concentric and monodomain configurations are formed in circular cross-sections and lateral planes, respectively; schematically shown in Fig. 1o. Note that the monodomain fingerprint gradually appearing from top and bottom toward the center in the POM images is due to the spatial average of concentric configuration progressively forming from the capillary wall towards the capillary center. In other words, the 2D fingerprint on the lateral plane provides insight into the three-dimensional configuration exiting inside the capillary (see Fig. 1a–l, o).

BLG and CNC are similar from various viewpoints; these BCLLCs are aqueous solutions of semi-rigid rod-like bio-colloidal LCs characterized by a long pitch length (p_∞,BLG = 43 µm and p_∞,CNC = 20 µm), high aspect ratio (\(\ell _{{\mathrm{BLG}}}\) = 652 nm and \(\ell _{{\mathrm{CNC}}}\) = 325 nm, D_BLG = 4 nm, D_CNC = 4.6 nm, \(\left( {\ell /D} \right)_{{\mathrm{BLG}}}\) = 163, and \(\left( {\ell /D} \right)_{{\mathrm{CNC}}}\) = 71), similar polydispersity, critical concentrations, and densities (Supplementary Note 2, Table 1)^{14,21,22,45,46}. Lastly, as estimated in this study, BLG and CNC possess similar rotational viscosity coefficients, L₁ Landau elastic constants, and coherence lengths (Tables 1 and 2). Surprisingly, although BLG and CNC have multiple physical properties that are similar and are confined into an identical capillary tube, D = 260 μm, they manifest remarkably different relaxation according to these three criteria:

The first difference is the characteristic time required for the spontaneous PN–N* transition during which the fibers equilibrate from the unwound state (i.e. non-equilibrium para-nematic) to the chiral ground state, see Fig. 1. BLG closely reaches the equilibrium state 4 days after capillary filling. In the time span of 4–7 days, relaxation has minor progress and defects may be released over this period; see Fig. 1a–f, m. The relaxation of CNC suspension only takes 1 day to reach equilibrium; see Fig. 1g–l, n. Hence, the relaxation time of BLG is nearly four times longer compared to CNC. It is important to notice that at the beginning of the relaxation process, when compared with BLG, CNC has more intact chiral helices near the walls; see Fig. 1b, h. This fact is also highlighted in Fig. 1m, n, where R, evolves from 0.6 to 1 as relaxation progresses for CNC, while it goes from 0.3 to 1 for BLG. Indeed, the higher initial relaxation progress is, the shorter time would be expected for achieving the relaxed state; thus, the higher initial relaxation progress of CNC, R = 0.6, certainly plays role in shortening the relaxation time. To achieve a quantitative comparison between the two relaxation behaviors, we compute the relaxation rates for the two systems. The relaxation progress of CNC evolves by 40% over 1 day for reaching the equilibrium point (R = 1), while it evolves by 70% over 4 days for BLG and therefore the relaxation rates are 40% and 17.5% per day, respectively, confirming that CNC relaxation is more than two times faster compared to BLG.

The second difference between these two systems involves the number of trapped defects at equilibrium. As shown in Fig. 1a–l, the ground state of BLG shows fewer defects compared to CNC. It has already been shown that, for a given pitch length, more defects emerge provided the geometric size increases⁴⁷, here the geometric size is the diameter of the cylindrical capillary. Similarly, at a fixed capillary diameter D = 260 μm, the number of defects increases when the pitch length is shorter. For BLG, p_∞,BLG = 43 μm, and for CNC, p_∞,CNC = 20 μm, corresponding to zero and four defects, respectively (see Fig. 1f, l). The ratio of geometric size to pitch length is thus an indicator for the number of generated defects; BLG relaxation gives rise to fewer defects compared to CNC suspension owing to \(\frac{D}{{p_{\infty ,\,{\mathrm{BLG}}}}} = 6\) and \(\frac{D}{{p_{\infty ,\,{\mathrm{CNC}}}}} = 13\). Another factor controlling the number of trapped defects is the relaxation time. Faster relaxation dynamics lead to more trapped defects as defects do not have time to be expelled. Thus, the CNC faster relaxation dynamic should also be taken to account as a promoter of trapped defects. Taken together, the number of defects is directly and inversely proportional to \(\frac{D}{{p_\infty }}\) and the relaxation time, respectively. Therefore, it is ideally expected that the defect-less ground state can be achieved as long as \(\frac{D}{{p_\infty }}\) and the relaxation time are sufficiently small and long, respectively. It should also be taken into consideration that the defect-less structure is achieved on a defined region of interest (260 µm × 260 µm) for BLG as shown in Figs. 1a–f and 2; however, it is impractical to reach the defect-less structure on a large domain (e.g. 600 µm × 260 µm) even after equilibration, see Supplementary Note 3.

Although the defect analysis discussed above was performed on the region of interest (260 µm × 260 µm), Supplementary Note 3 demonstrates that the chosen system size is statistically large enough to extend the concluded results regarding the number of trapped defects to larger regions. As shown in Supplementary Fig. 3, the number of defects trapped in the BLG system is less compared to CNC on a larger region (600 µm × 260 µm) after equilibration (10 days for BLG and 3 days for CNC). Additionally, the defects existing in the capillary are mobile and thus can translate in and/or out the system investigated (260 µm × 260 µm); however, the results already discussed are always statistically valid (see Supplementary Movies 1 and 2 and Supplementary Note 3).

Finally, these two materials differ on how the speed of relaxation changes over time. As shown in Fig. 1m, BLG relaxes over consecutive steps consisting of four plateaus, which we described as slow–fast relaxation behavior. During each plateau, there is no discernible change in the total area of the striped zone, reflecting that cholesteric phase formation slows down considerably, as discussed below. However, in the CNC suspension, the relaxation is characterized by a smooth behavior, where no clear plateau can be detected (see Fig. 1n).

The liquid-crystal rotational viscosity is the resistance to rotations of the average macroscopic director orientation^32,33. For this reason, it is expected that the longer relaxation time observed for BLG can be attributed to higher rotational viscosity of BLG. However, there has not yet been any report on rotational viscosities and relaxation trends of these two bio-colloids, and the physical origins behind the different behaviors remain up to date unexplored. The solid lines shown in Fig. 1m, n are the predictions obtained by direct numerical simulations of the time-dependent Q-tensor continuum model of cholesteric liquid crystals that describes the total free-energy minimization. In our work, the net free energy of the system is comprised of free-energy functionals given by the well-established continuum theories of Landau-de Gennes (LdG) and Frank-Oseen-Mermin (FOM)^25,32,48,49 (see section “Direct numerical simulation”). As shown in Fig. 1m, n, the adopted theoretical approach predicts both the slow–fast and smooth relaxation dynamics for BLG and CNC, respectively. Hence, we rely on continuum liquid-crystal theory to first explore the physics behind the observations and secondly to estimate viscoelastic properties, including rotational viscosity coefficient which allows us rationalizing the fast and slow relaxation behaviors of CNC and BLG, respectively.

Mechanisms of BLG and CNC relaxations

As shown in Fig. 2, the theoretical and experimental results consistently show that cholesteric layers (i.e. the striped bands in POM images) are gradually formed from the top and bottom walls on the lateral plane. As can be seen in our results, the relaxation (the PN–N* transition) spontaneously takes place through the chiral front propagation; the cholesteric fingerprints radially propagate from the circular wall inward through the unwound para-nematic medium until the concentric configuration is achieved. This configuration is expected since the capillary diameter is larger than pitch length^17,19, \(\frac{D}{{p_\infty }} = 6\) (Supplementary Note 4 and Movie 3).

The mechanism of BLG relaxation generally consists of two phases (Supplementary Movies 3 and 4) that can be described as

Phase (I): This phase takes place over a considerably short time span in the early relaxation. During Phase (I), all fibers, which are in the para-nematic state, lose their initial order parameter, S_i = 0.6 (ref. ⁴²), and then turn into a low-order-parameter para-nematic state (nearly isotropic), S_d,BLG ≈ 0.33 (Fig. 2 and Supplementary Movies 3 and 4).

Phase (II): Right after rapid formation of the para-nematic medium with a low-order parameter (i.e. Phase (I)), relaxation goes through Phase (II) in which a circular chiral front propagates and rewinds the fibers. As can be seen in Supplementary Movies 3 and 4, Phase (II) in BLG relaxation follows a time-periodic mechanism in which one half-pitch cholesteric layer is formed. The formation of each half-pitch consists of four stages; these stages are discussed in Supplementary Note 5.

The slow–fast relaxation observed for BLG consists of four sigmoid-like steps, and each of which ideally corresponds to the formation of a circular half-pitch, \(\frac{{p_\infty }}{{\mathrm{2}}}\). In particular, the label numbers B₂, B₃, B₄, and B₅ in Fig. 1m and Fig. 2 correspond to the circular formation of \(\frac{{{\mathrm{3}}p_\infty }}{{\mathrm{2}}}\), \(\frac{{{\mathrm{4}}p_\infty }}{{\mathrm{2}}}\), \(\frac{{{\mathrm{5}}p_\infty }}{{\mathrm{2}}}\), and \(\frac{{{\mathrm{6}}p_\infty }}{{\mathrm{2}}}\), respectively (see more details in Supplementary Note 4). This behavior is confirmed by simulations and is consistent with the experimental analysis concerning both fibers configuration and trapped defects; however, the simulation prediction of cholesteric layers formation is slightly overestimated. For this reason, the theoretical prediction of relaxation progress, R, is slightly higher than the experimental data.

Figure 3 illustrates representative images of the equilibration sequence for CNC fibers, showing that this system relaxes through similar mechanisms, achieving concentric configuration as expected from previous works^17,19 (see Supplementary Note 4). During Phase (I), the order parameter of CNC fibers that are in the para-nematic medium is dramatically dropped to S_d,CNC ≈ 0 at the beginning of relaxation despite their initial order parameter S_i = 0.6 (ref. ⁴²) and as a consequence, isotropic phase emerges from the para-nematic medium, followed by Phase (II), where the chiral front propagates into an isotropic medium (Supplementary Movie 5).

According to the LdG theory, the critical order parameter at the order–disorder phase transition can be considered as S_c = 0.25 (ref. ³²), which means that, if S > S_c fibers possess orientational ordering, otherwise fibers lose their correlations and the phase becomes isotropic (see Supplementary Note 7). The simulation results reveal that, during the early relaxation, order parameters of BLG and CNC fibers in the para-nematic mediums have dropped to S_d,BLG ≈ 0.33 and S_d,CNC ≈ 0, respectively. Hence, at the beginning of the relaxation, the fibers in the para-nematic state in the middle of the capillary decrease their order parameter during Phase (I) and the solutions become weakly anisotropic and nearly isotropic for BLG and CNC, respectively. These theoretical predictions are in excellent agreement with POM images because the dark zone in POM images of BLG is slightly blended with a faint reddish color indicating that the fibers therein possess an extremely week orientational ordering and are aligned parallel to the central axis of the capillary, see Figs. 1a–f and Fig.  2c, e, g, i, k. On the other hand, the middle of POM images of CNC is almost dark without any other color denoting that the fibers therein are in the completely isotropic phase, see Fig. 1g–l and Fig. 3c, e, g. Consequently, this supports the assumption we made in the experimental analysis on the dark zones observed in the microscopy images; the dark zones should be considered isotropic areas or para-nematic with extremely low-order parameter, and not nematic nor cholesteric with axes parallel to the light path.

Understanding the physical origins of relaxation mechanisms

As above-mentioned, it is found that the relaxation mechanisms can generally be described by two consecutive phases. This section reveals the physics behind the explored mechanisms in terms of the free-energy landscape.

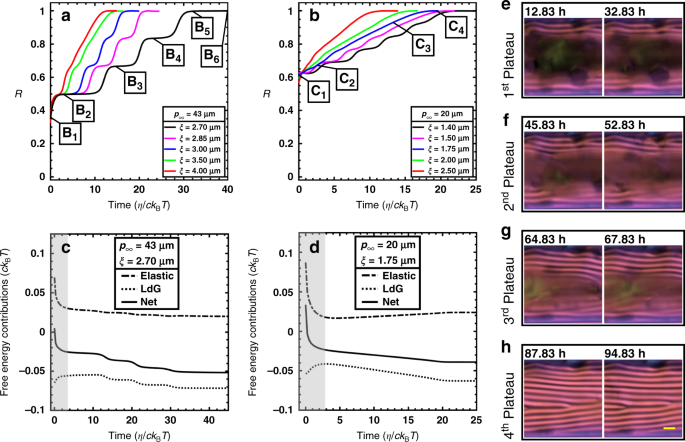
According to Eqs. (7–9), two factors mainly govern relaxation dynamics: pitch length and coherence length. For a given cylindrical capillary, the impacts of these factors are shown in Fig. 4a, b. The simulations suggest that smooth relaxation can change to slow–fast relaxation and vice versa. For instance, for a given pitch length, smooth relaxation gradually switches to (emerges from) slow–fast relaxation, upon decreasing (increasing) the coherence length.

a, b Parametric analyses of the normalized relaxation progress, R, showing that smooth relaxation dynamics arise, provided coherence length is greater than a threshold. η stands for the rotational viscosity coefficient. c, d The interplay between homogeneous and elastic free energies, and the resulting net free energy. The gray-hatched zones indicate the period over which the order parameter of the para-nematic phase is dropped, Phase (I), and the remaining white-hatched zones correspond to front propagation, Phase (II). During the former and the latter, as can be appreciated by net free-energy behavior, elastic and homogeneous contributions mainly control net free energy, respectively. Note that all graphs exhibit the spatial-averaged quantities and the panels c and d correspond to the BLG and CNC relaxations, respectively. e–h POM images showing no significant change in the cholesteric zone during each of the four BLG plateaus marked in Fig. 1m. These POM images were experimentally acquired using the LC PolScope device. Scale bar is p_∞ = 43 µm.

In liquid-crystalline phases, the coherence length ξ describes the distance over which long-range orientational order varies⁴⁹ and is expected to be in the nano-meter range for small-sized rod-shaped mesogens such as 5CB (\(\ell _{{\mathrm{5CB}}} = {\mathrm{1}}{\mathrm{.8}}\,{\mathrm{nm}}\) and \(\xi _{{\mathrm{5CB}}} \approx {\mathrm{7}}\,{\mathrm{nm}}\))⁵⁰. In particular, ξ is directly correlated with length of rod-shaped mesogen⁵¹, and ξ is thus expected to be in the micro-meter range for long fibrous mesogens since their contour lengths are two orders of magnitude longer compared to small-sized mesogens (e.g. \(\ell _{{\mathrm{BLG}}} = {\mathrm{652}}\,{\mathrm{nm}}\) and \(\ell _{{\mathrm{CNC}}} = {\mathrm{325}}\,{\mathrm{nm}}\)). As illustrated in Fig. 4a, b, the parametric analyses shed light on the fact that the observed relaxation dynamics are induced for a micro-meter range of coherence length defined in Eq. (2). The coherence lengths that best fit the experimental data of BLG and CNC shown in Fig. 1m, n are: ξBL = 2.7 μm and ξ_CNC = 1.75 μm, respectively.

Before proceeding in elucidating the mechanism of cholesteric layers formation, it is important to quantify the impact of order parameter reduction on the free-energy contributions. The homogeneous and gradient elastic free-energy contributions to the net free energy are given by the LdG and FOM theories are^{16,25,52,53,54,55}:

The homogeneous free energy f_h decreases when the order parameter increases from a low to the equilibrium value; therefore, this contribution promotes orientational ordering. The gradient elastic free energy f_g is the energy cost of orientational configuration and is minimum when the ground state is achieved. The decreasing order parameter results in decreasing f_g since Eq. (9) shows that there is a factor of S in all the terms of f_g (see Supplementary Note 8 for more discussion about the impact of order parameter reduction on the free-energy contributions). In partial summary, the order parameter reduction increases the homogeneous contribution and decreases the gradient elastic contribution.

As mentioned earlier, the mechanisms behind the relaxation dynamics are described by two consecutive phases as follows:

Phase (I): early relaxation depicted by the gray-hatched zones in Fig. 4c, d. During this short period, fibers in the para-nematic medium decrease their order parameter. This unexpected behavior can be explained by analyzing the free-energy contributions. The ground state is inherently chiral nematic, thus the para-nematic alignment, which represents unwound chiral helices, gives rise to an excess elastic free energy and, in consequence, rises the net free energy immediately before relaxation starts; see t = 0 in Fig. 4c, d. Because the elastic free energy is weighted by the coherence length squared and the para-nematic alignment is unfavorable owing to the concentric ground state, the excess elastic energy is intensified by increasing of coherence length and/or decreasing of pitch length (see Supplementary Notes 8 for the detailed discussion).

To reduce the total excess energy imposed by the initial para-nematic alignment, fibers existing in the para-nematic phase decrease their order parameter to decrease the dominant gradient elastic free energy, although an order parameter reduction is energetically unfavorable for the less costly homogeneous contribution (see Fig. 4c, d). The order parameter of the para-nematic medium thus drops to a low value, S_d, shortly after the relaxation starts. Therefore, the more excess elastic energy, the more the order parameter of the para-nematic medium should drop. Taken altogether, the pitch length and coherence length are directly and inversely proportional to the order parameter of the para-nematic medium, S_d, respectively (Supplementary Notes 8 and 9).

Since S_d is either close to or lower than the order parameter at the phase transition, S_c = 0.25, a dark zone emerges and persists in the POM images while the relaxation continues; for example, Fig. 1a, b, g, h shows that Phase (I) is completed during the first 15–20 min for both BLG and CNC. When the emergence of dark zones in the time-series POM images is completed, Phase (I) terminates. Also, during the early relaxation, i.e., Phase (I), the order parameter reduction largely affects the gradient elastic contributions compared to homogeneous contribution; hence order parameter reduction results in reducing the net free energy (see Fig. 4c, d).

Phase (II): front propagation illustrated in Fig. 4c, d. As the front propagates inward through the para-nematic medium with the order parameter of S_d, the dark zone progressively shrinks, see Figs. 1a–l, 2, 3 and 4e–h. S_d, which depends on both the pitch length and the coherence length, is a key factor to determine whether relaxation dynamics become slow–fast or smooth. Numerical simulation supported by experimental observations shows that if S_d ≈ 0, the para-nematic phase becomes essentially isotropic and the smooth relaxation takes place as discussed for CNC relaxation. As S_d gradually increases, the plateaus are more pronounced. Eventually, relaxation ends up with slow–fast mode in cases that S_d ≈ 0.3–0.4 like such as BLG relaxation having S_d,_BLG = 0.33 (Supplementary Note 9). As can be seen in Fig. 4e–h, during the plateaus, there is an insignificant change in the formed cholesteric layers, which slows down the relaxation.

Because, as already explained, S_d directly and inversely depends on the pitch length and coherence length, we conclude that a decrease (an increase) in the pitch length and/or increase (decrease) of the coherence length drives the relaxation toward smooth (slow–fast) dynamics (see Supplementary Fig. 12). Finally, regardless of the S_d value, Phase (II) ends by reaching the self-selected ground state of a concentric due to \(\frac{D}{{p_\infty }} > 1\), which is in agreement with previous studies^17,19.

In addition to the coherence length and pitch length, geometric confinement is expected to have a significant impact on relaxation (Supplementary Note 10). This effect is beyond the scope of this work, which is based on a single diameter capillary.

Properties estimation and relaxation time controllers

The quantitative agreement between experimental observations and theoretical predictions (Fig. 1m, n) provides a way to obtain quantitative estimates of the rotational viscosity coefficient η and coherence length ξ. Knowing the coherence length^{25,49,53,56,57,58,59,60},

where k_B and T stand for Boltzmann’s constant and temperature, it is then possible to calculate the elastic constant L₁ (Supplementary Note 11).

Table 1 shows that the equilibrium order parameter computed by numerical simulation is consistent with the results of the analytical equation formulated in previous theoretical studies^25,49. The elastic constant L₁, which is related to Frank’s elastic constants⁵², is in the range used in other studies^24,61,62,63. To the best of authors’ knowledge, there has not been any report in the literature concerning rotational viscosity coefficients of BCLLCs. There, however, exists a few studies where rotational viscosity coefficients have experimentally been measured for large molecular-weight LCs, reporting 2.8 × 10⁵P and 9.9 × 10⁵P for PBLG and mesogenic polyesters, respectively^35,36. As justified in ref. ³⁶, in comparison to thermotropic LCs, BCLLCs possess a large rotational viscosity coefficient because the relaxation time of thermotropic LCs is in range of milliseconds while BCLLCs ranges from hours to days.

Having rotational viscosity coefficients of BLG and CNC estimates, we can answer whether lower rotational viscosity of CNC is the reason behind its fast relaxation dynamic. The rotational viscosity γ is^25,32

and increases with decreasing S. The results shown in Table 2 confirm that the rotational viscosity of BLG is larger than that of CNC throughout the relaxation in the order of \(\frac{{\gamma _{{\mathrm{CNC}}}}}{{\gamma _{{\mathrm{BLG}}}}} \approx 0.57 - 0.64\). Therefore, lower rotational viscosity of CNC speeds the relaxation.

The free-energy driving force also contributes to the relaxation kinetics as the phase ordering rate is (see section “Direct numerical simulation” and Eq. (5))

The difference between initial and equilibrium net free energy is representative of the free-energy driving force, ΔF. Based on Fig. 4c, d, we conclude that the free-energy driving force for relaxation of CNC is also larger than that of BLG, \(\frac{{{\Delta}F_{{\mathrm{CNC}}}}}{{{\Delta}F_{{\mathrm{BLG}}}}} = 1.28\). Consequently, CNC relaxation is faster because of two synergetic effects: (1) lower rotational viscosity and (2) higher free-energy driving force.